Iprojekthi ye-Euler luthotho lweengxaki ezinomdla zenkqubo, zihlala zinemvelaphi yemathematics. Iingxaki zihlala zibekwa ngohlobo lokuba ii-algorithms ezinobunkunkqele kufuneka ziphuhlisiwe ukulungiselela ukufezekisa injongo ngexesha elifanelekileyo lokubaleka. Namhlanje sisombulula ingxaki ye-15: Iindlela zeLatice , apho unokufumana khona isisombululo ngeendlela ezilula zokudibanisa.
Umbuzo ulandelayo:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
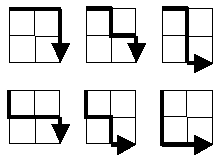
Ingxaki inokwenziwa ngendlela eyahlukileyo: Into efunekayo ngamandla eseti esezantsi yazo zonke iindlela
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Sijongene nengxaki elula yokudibanisa apho sisebenzisa imodeli ye-urn (ngaphandle kokutshintsha ngaphandle kokuhoya iodolo). Ngoku sinomdla ngqo kwezi ndlela zibambe ukuba \(R\) kunye \(D\) ngokufanayo rhoqo. Oku kubangela konke ukudityaniswa okunokwenzeka:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Ye \(n=20\) siyifumana:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Singayandisa ingxaki kwiigridi ezingezizo ezesikwere. Esi sisombululo silandelayo sisebenzisa ukubala kwi-PHP ngoncedo lwe- bcmath enexesha lokubaleka le- \( O(n) \) ngefomathi yokufaka "Inani lamatyala ovavanyo, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
Ngendlela , zonke iingxaki zeProjekthi ye-Euler zinokusonjululwa kwi-Intanethi kwindawo ekucetyiswa ukuba yiHackerRank .