Project Euler è una serie di eccitanti problemi di programmazione, spesso con un background matematico. I problemi sono spesso posti in modo tale che algoritmi sofisticati devono essere sviluppati per raggiungere l'obiettivo in un tempo ragionevole. Oggi risolviamo il problema 15: Percorsi reticolari , per i quali è possibile trovare la soluzione con semplici mezzi combinatori.
La domanda è la seguente:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
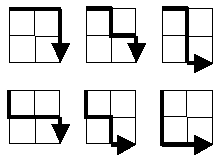
Il problema può anche essere formulato in modo diverso: ciò che serve è la potenza del sottoinsieme di tutti i percorsi
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Questo è un semplice problema combinatorio in cui utilizziamo il modello urna (senza sostituire e senza considerare l'ordine). Ora siamo interessati proprio a quei percorsi per i quali vale che \(R\) e \(D\) esattamente con la stessa frequenza. Ciò si traduce in tutte le possibili combinazioni:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Per \(n=20\) otteniamo:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Possiamo estendere il problema a griglie non quadrate. La seguente soluzione implementa un calcolo in PHP con l'aiuto di bcmath con un runtime di \( O(n) \) con il formato di input "Numero di casi di test, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
A proposito, tutti i problemi del progetto Euler possono essere risolti anche online sul sito HackerRank consigliato.