A Project Euler izgalmas programozási problémák sora, gyakran matematikai háttérrel. A problémákat gyakran úgy vetik fel, hogy kifinomult algoritmusokat kell kidolgozni a cél ésszerű időn belüli elérése érdekében. Ma megoldjuk a 15. feladatot: Rácspályák , amelyekre egyszerű kombinatorikus eszközökkel megtalálhatja a megoldást.
A kérdés a következő:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
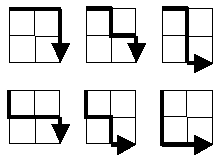
A probléma másként is megfogalmazható: Minden út részhalmazának erejére van szükség
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Ez egy egyszerű kombinatorikus probléma, amelyben az urna modellt használjuk (cseré nélkül és a sorrend figyelembevétele nélkül). Most éppen azok az utak érdekelnek minket, amelyeknél az áll, hogy \(R\) és \(D\) pontosan azonos gyakorisággal \(D\) . Ez minden lehetséges kombinációt eredményez:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
\(n=20\) esetén megkapjuk:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Kiterjeszthetjük a problémát a nem négyzet alakú rácsokra is. A következő megoldás egy számítást hajt végre PHP-ben a bcmath segítségével \( O(n) \) futási \(n_1\) száma, \(n_1\) \(m_1\) , ..." bemeneti formátummal.:
47bb78215ee0531a787bb5034652eaf4
Egyébként az Euler Project minden problémája online is megoldható az ajánlott HackerRank oldalon.