Project L. Euler est a programming seriem excitando problems, saepe cum mathematica background. Et difficultates quas saepe sophisticated algorithms ita ut ad consequi metam est ut developed per rationabile tempus. Hodie solvere problema XV: cancellos per vias rectas , ubi vos can reperio solutio simplex cum minime combinationum.
Quaestio est, sequitur quod:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
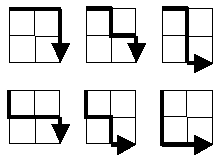
Et quaestio potest etiam esse exceptione utitur: Quod est opus sit potentia copia omnium impios semitae ipsius
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Hoc problema est simplex combinationum in qua urna aurea uti exemplar (sine repositoque et non attendens ad ordinem). Nos nunc pressius interested in his quæ ad impios semitae ipsius, semper verum est \(R\) et \(D\) prorsus idem frequency. Hic omnium possibilium combinationum praecessi:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Nam \(n=20\) dabimus tibi:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Extend possumus quaestio est non-quadratus grids. Poterit adhiberi solutio telis conficitur ope calculi in PHP bcmath cum runtime \( O(n) \) Cum initus forma "Number of test casibus, \(n_1\) \(m_1\) : ...":
47bb78215ee0531a787bb5034652eaf4
Per viam, de omnibus problems can quoque solvitur online Leonhard Euler Project suadetur ex HackerRank site.