प्रोजेक्ट यूलर एक गणितीय पृष्ठभूमि के साथ अक्सर रोमांचक प्रोग्रामिंग समस्याओं की एक श्रृंखला है। समस्याओं को अक्सर इस तरह से पेश किया जाता है कि एक उचित समय में लक्ष्य को प्राप्त करने के लिए परिष्कृत एल्गोरिदम विकसित किया जाना चाहिए। आज हम समस्या 15 का समाधान करते हैं : जालीदार रास्ते , जहाँ आप सरल दहनशील साधनों के साथ समाधान पा सकते हैं।
प्रश्न इस प्रकार है:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
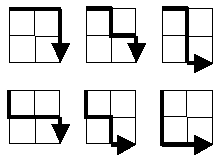
समस्या को अलग तरीके से भी तैयार किया जा सकता है: जो आवश्यक है वह सभी रास्तों के सबसेट की शक्ति है
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
यह एक सरल कॉम्बिनेटोरियल समस्या है जिसमें हम कलश मॉडल का उपयोग करते हैं (बिना जगह पर और ऑर्डर पर विचार किए)। अब हम ठीक उन रास्तों में रुचि रखते हैं, जिनके लिए यह वही \(R\) और \(D\) रखता \(D\) ठीक उसी आवृत्ति के साथ। यह सभी संभव संयोजनों का परिणाम है:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
\(n=20\) हमें मिलता है:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
हम समस्या को गैर-वर्ग ग्रिड तक बढ़ा सकते हैं। निम्नलिखित समाधान के औजार की मदद से PHP में एक गणना bcmath के क्रम के साथ \( O(n) \) इनपुट प्रारूप के साथ "परीक्षण मामलों की संख्या, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
वैसे, हैकर प्रोजेक्ट की सभी समस्याओं को अनुशंसित हैकरैंक साइट पर ऑनलाइन हल किया जा सकता है।