প্রজেক্ট অয়লার প্রায়শই গাণিতিক পটভূমি সহ আকর্ষণীয় প্রোগ্রামিং সমস্যার একটি সিরিজ। সমস্যাগুলি প্রায়শই এমনভাবে উত্থাপিত হয় যে একটি উপযুক্ত সময়ে লক্ষ্য অর্জনের জন্য পরিশীলিত অ্যালগরিদমগুলি বিকাশ করতে হয়। আজ আমরা সমস্যার সমাধান 15: জাল পথ , যেখানে আপনি সহজ সমন্বয়কারী উপায় দিয়ে সমাধানটি সন্ধান করতে পারেন।
প্রশ্নটি নিম্নরূপ:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
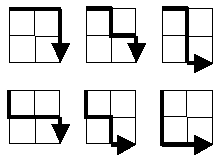
সমস্যাটিও আলাদাভাবে তৈরি করা যেতে পারে: যা দরকার তা হ'ল সমস্ত পথের উপসেটের শক্তি
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
এটি একটি সাধারণ সংমিশ্রণীয় সমস্যা যার মধ্যে আমরা ভর্নের মডেলটি ব্যবহার করি (প্রতিস্থাপন ছাড়াই এবং আদেশ বিবেচনা না করে)। আমরা এখন সেই পাথগুলিতে অবিকল আগ্রহী যেগুলির জন্য এটি ধারণ করে যে frequency \(R\) এবং \(D\) একই ফ্রিকোয়েন্সি সহ ঠিক \(D\) । এটি সমস্ত সম্ভাব্য সংমিশ্রণের ফলাফল:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
\(n=20\) আমরা পাই:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
আমরা সমস্যাটি নন-স্কোয়ার গ্রিডগুলিতে প্রসারিত করতে পারি। নিম্নলিখিত সমাধান কার্যকরী সাহায্যে পিএইচপি একটি হিসাব bcmath একটি রানটাইম সঙ্গে \( O(n) \) ইনপুট ফর্ম্যাট সঙ্গে "পরীক্ষা মামলার নম্বর, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
যাইহোক , এলার প্রকল্পের সমস্ত সমস্যাগুলিও প্রস্তাবিত হ্যাকারর্যাঙ্ক সাইটে অনলাইনে সমাধান করা যেতে পারে।