Project Euler , genellikle matematiksel bir geçmişe sahip bir dizi heyecan verici programlama problemidir. Sorunlar genellikle, amaca makul bir sürede ulaşmak için karmaşık algoritmaların geliştirilmesi gerekecek şekilde ortaya çıkar. Bugün problem 15'i çözüyoruz: Çözümü basit kombinatoryal yollarla bulabileceğiniz Kafes yolları .
Soru aşağıdaki gibidir:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
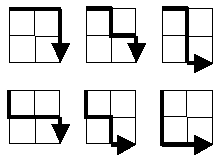
Sorun ayrıca farklı şekilde formüle edilebilir: İhtiyaç duyulan şey, tüm yolların alt kümesinin gücüdür.
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Bu, urn modelini kullandığımız basit bir kombinatoryal problemdir (değiştirmeden ve sırayı dikkate almadan). Şimdi, \(R\) ve \(D\) tam olarak aynı frekansta \(D\) iddia ettiği yollarla ilgileniyoruz. Bu, tüm olası kombinasyonlarla sonuçlanır:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
\(n=20\) için:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Sorunu kare olmayan ızgaralara genişletebiliriz. Aşağıdaki çözüm, PHP'de "Test durumlarının sayısı, \(n_1\) \(m_1\) , ..." girdi biçimiyle \( O(n) \) çalışma zamanıyla bcmath kullanarak bir hesaplama uygular.:
47bb78215ee0531a787bb5034652eaf4
Bu arada, Euler Projesi'nin tüm sorunları, önerilen HackerRank sitesinde çevrimiçi olarak da çözülebilir.