IProject Euler iluchungechunge lwezinkinga ezijabulisayo zohlelo, imvamisa enesizinda sezibalo. Izinkinga zivame ukwenziwa ngendlela yokuthi kufanele kwenziwe ama-algorithm eyinkimbinkimbi ukuze kuzuzwe inhloso ngesikhathi esifanele. Namuhla sixazulula inkinga ye-15: Izindlela ze-Lattice , lapho ungathola khona isisombululo ngezindlela ezilula zokuhlanganisa.
Umbuzo ulandelayo:
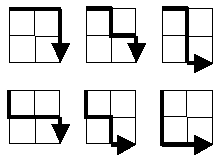
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
Inkinga nayo ingenziwa ngendlela ehlukile: Okudingekayo ngamandla we-subset yazo zonke izindlela
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Sisebenzelana lapha nenkinga elula yokuhlanganisa lapho sisebenzisa khona imodeli ye-urn (ngaphandle kokufaka esikhundleni futhi ngaphandle kokunaka i-oda). Manje sesinentshisekelo kuzo lezo zindlela okubambe kuzo ukuthi \(R\) no \(D\) ngokuvama okufanayo. Lokhu kubangela yonke inhlanganisela engenzeka:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Okwe \(n=20\) sithola:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Singayandisa inkinga kuma-grid angasikwele. Isixazululo esilandelayo sisebenzisa ukubalwa ku-PHP ngosizo lwe- bcmath nesikhathi sokusebenza se- \( O(n) \) ngefomethi yokufaka "Inombolo yamacala wokuhlola, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
Ngendlela, zonke izinkinga ze-Euler Project nazo zingaxazululwa ku-inthanethi kusiza esinconyiwe seHackerRank .