Project Euler adalah serangkaian masalah pemrograman yang menarik, seringkali dengan latar belakang matematika. Masalah sering diajukan sedemikian rupa sehingga algoritma yang canggih harus dikembangkan untuk mencapai tujuan dalam waktu yang wajar. Hari ini kita menyelesaikan masalah 15: Jalur kisi , di mana Anda dapat menemukan solusi dengan cara kombinatorial sederhana.
Pertanyaannya adalah sebagai berikut:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
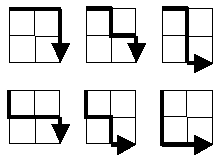
Masalahnya juga dapat dirumuskan secara berbeda: Yang dibutuhkan adalah kekuatan subset dari semua jalur
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Ini adalah masalah kombinatorial sederhana di mana kami menggunakan model guci (tanpa mengganti dan tanpa mempertimbangkan urutan). Kami sekarang tertarik pada jalur yang dianggap \(R\) dan \(D\) persis dengan frekuensi yang sama. Ini menghasilkan semua kemungkinan kombinasi:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Untuk \(n=20\) kita dapatkan:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Kita dapat memperluas masalah ke kisi non-persegi. Solusi berikut mengimplementasikan kalkulasi dalam PHP dengan bantuan bcmath dengan runtime \( O(n) \) dengan format input "Jumlah kasus uji, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
Omong- omong, semua masalah Proyek Euler juga dapat diselesaikan secara online di situs HackerRank yang direkomendasikan.