Project Euler مجموعه ای از مشکلات جالب برنامه نویسی است که غالباً دارای پیشینه ریاضی است. مشکلات اغلب به گونه ای مطرح می شوند که الگوریتم های پیچیده برای دستیابی به هدف در مدت زمان معقول باید توسعه داده شوند. امروز ما مسئله 15: راههای شبکه را حل می کنیم ، جایی که می توانید راه حل را با استفاده از روش ترکیبی ساده پیدا کنید.
سوال به شرح زیر است:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
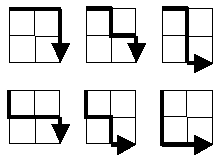
این مسئله همچنین می تواند به صورت متفاوت تنظیم شود: آنچه مورد نیاز است ، قدرت زیر مجموعه همه مسیرها است
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
این یک مسئله ترکیبی ساده است که در آن ما از مدل urn (بدون تعویض و بدون در نظر گرفتن ترتیب) استفاده می کنیم. اکنون دقیقاً به آن مسیرهایی علاقه مندیم که مشخص می کند \(R\) و \(D\) دقیقاً \(D\) همان فرکانس \(D\) . این نتیجه در تمام ترکیبات ممکن است:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
برای \(n=20\) دریافت می کنیم:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
ما می توانیم مشکل را به شبکه های غیر مربعی گسترش دهیم. راه حل زیر با استفاده از bcmath با زمان اجرا \( O(n) \) با قالب ورودی "تعداد موارد آزمایشی ، \(n_1\) \(m_1\) ...)" با استفاده از bcmath یک محاسبه را اجرا می کند:
47bb78215ee0531a787bb5034652eaf4
ضمناً ، همه مشکلات پروژه اویلر نیز می تواند به صورت آنلاین در سایت پیشنهادی HackerRank حل شود.