Project Euler- ը ծրագրավորման հետաքրքիր խնդիրների շարք է, հաճախ մաթեմատիկական ֆոնի վրա: Խնդիրները հաճախ առաջադրվում են այնպես, որ բարդ ալգորիթմներ մշակվեն ՝ նպատակին հասնելու ողջամիտ ժամկետում հասնելու համար: Այսօր մենք լուծում ենք 15-րդ խնդիրը. Անցային ուղիներ , որտեղ լուծումը կարող եք գտնել պարզ կոմբինացիոն միջոցներով:
Հարցը հետեւյալն է:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
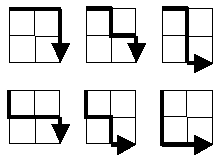
Խնդիրը կարող է նաև այլ կերպ ձևակերպվել. Անհրաժեշտ է բոլոր ուղիների ենթաբազմության հզորությունը
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Սա պարզ կոմբինացիոն խնդիր է, որում մենք օգտագործում ենք ուրանի մոդելը (առանց փոխարինելու և առանց կարգը հաշվի առնելու): Մեզ հիմա հետաքրքրում են հենց այն ուղիները, որոնց համար պնդում է, որ \(R\) և \(D\) ճիշտ նույն հաճախականությամբ: Սա հանգեցնում է բոլոր հնարավոր համադրությունների:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Համար \(n=20\) մենք ստանում ենք:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Մենք կարող ենք խնդիրը տարածել ոչ քառակուսի ցանցերի վրա: Հետևյալ լուծումը իրականացնում է հաշվարկ PHP- ում ` bcmath- ի միջոցով \( O(n) \) գործարկման եղանակով` «Փորձնական դեպքերի քանակը, \(n_1\) \(m_1\) , ...» մուտքագրման ձևաչափով::
47bb78215ee0531a787bb5034652eaf4
Ի դեպ, Euler Project- ի բոլոր խնդիրները կարող են լուծվել նաև առցանց `առաջարկվող HackerRank կայքում: