Project Euler est une série de problèmes de programmation passionnants, souvent avec une formation mathématique. Les problèmes sont souvent posés de telle manière que des algorithmes sophistiqués doivent être développés pour atteindre l'objectif dans un délai raisonnable. Aujourd'hui, nous résolvons le problème 15: les chemins de treillis , où vous pouvez trouver la solution avec des moyens combinatoires simples.
La question est la suivante:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
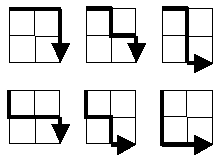
Le problème peut également être formulé différemment: il faut la puissance du sous-ensemble de tous les chemins
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Il s'agit d'un problème combinatoire simple dans lequel nous utilisons le modèle urne (sans remplacer et sans considérer l'ordre). Nous nous intéressons maintenant précisément aux chemins pour lesquels il soutient que \(R\) et \(D\) exactement avec la même fréquence. Il en résulte toutes les combinaisons possibles:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Pour \(n=20\) nous obtenons:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Nous pouvons étendre le problème aux grilles non carrées. La solution suivante implémente un calcul en PHP à l'aide de bcmath avec un runtime de \( O(n) \) avec le format d'entrée "Nombre de cas de test, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
À propos, tous les problèmes du projet Euler peuvent également être résolus en ligne sur le site HackerRank recommandé.