Проект Ейлера - це низка захоплюючих проблем програмування, часто з математичним досвідом. Проблеми часто ставляться таким чином, що для досягнення мети в розумні терміни доводиться розробляти складні алгоритми. Сьогодні ми вирішуємо задачу 15: Lратчасті шляхи , де ви можете знайти рішення простими комбінаторними засобами.
Питання полягає в наступному:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
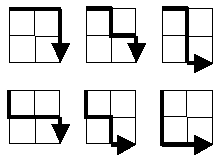
Проблему також можна сформулювати по-різному: потрібна потужність підмножини всіх шляхів
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Тут ми маємо справу з простою комбінаторною проблемою, в якій ми використовуємо модель урни (без заміни та не звертаючи уваги на порядок). Зараз нас цікавлять саме ті шляхи, для яких, на його думку, \(R\) та \(D\) точно з однаковою частотою. Результатом цього є всі можливі комбінації:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Для \(n=20\) отримуємо:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Ми можемо поширити проблему на неквадратні сітки. Наступне рішення реалізує обчислення в PHP за допомогою bcmath з часом виконання \( O(n) \) із вхідним форматом "Кількість тестових випадків, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
До речі, всі проблеми проекту Ейлера також можна вирішити в Інтернеті на рекомендованому сайті HackerRank .