Project Euler is een reeks opwindende programmeerproblemen, vaak met een wiskundige achtergrond. De problemen worden vaak zo gesteld dat geavanceerde algoritmen ontwikkeld moeten worden om het doel binnen een redelijke tijd te bereiken. Vandaag lossen we probleem 15 op: Roosterpaden , waarvoor u de oplossing kunt vinden met eenvoudige combinatorische middelen.
De vraag is als volgt:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
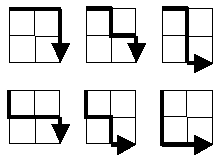
Het probleem kan ook anders worden geformuleerd: wat nodig is, is de kracht van de subset van alle paden
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Dit is een eenvoudig combinatorisch probleem waarbij we het urnenmodel gebruiken (zonder vervanging en zonder rekening te houden met de bestelling). We zijn nu geïnteresseerd in precies die paden waarvoor geldt dat \(R\) en \(D\) precies met dezelfde frequentie voorkomen. Dit resulteert in alle mogelijke combinaties:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Voor \(n=20\) krijgen we:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
We kunnen het probleem uitbreiden naar niet-vierkante roosters. De volgende oplossing implementeert een berekening in PHP met behulp van bcmath met een runtime van \( O(n) \) met het invoerformaat "Aantal testgevallen, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
Overigens kunnen alle problemen van het Euler Project ook online worden opgelost op de aanbevolen HackerRank- site.