Projekto Euler estas serio de ekscitaj programaj problemoj, ofte kun matematika fono. La problemoj ofte staras tiel, ke oni devas disvolvi sofistikajn algoritmojn por atingi la celon en racia tempo. Hodiaŭ ni solvas problemon 15: Kradaj vojoj , kie vi povas trovi la solvon per simplaj kombinaj rimedoj.
La demando estas jena:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
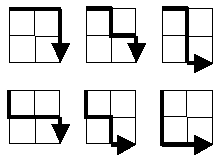
La problemo ankaŭ povas esti formulita alimaniere: Necesas la potenco de la subaro de ĉiuj vojoj
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Ĉi tio estas simpla kombina problemo, en kiu ni uzas la urnan modelon (sen anstataŭigi kaj sen konsideri la ordon). Ni nun interesiĝas ĝuste pri tiuj vojoj, por kiuj ĝi diras, ke \(R\) kaj \(D\) ĝuste kun la sama ofteco. Ĉi tio rezultigas ĉiujn eblajn kombinaĵojn:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Por \(n=20\) ni ricevas:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Ni povas etendi la problemon al ne-kvadrataj kradoj. La sekva solvo efektivigas kalkulon en PHP kun la helpo de bcmath kun rultempa tempo de \( O(n) \) kun la eniga formato "Nombro de testkazoj, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
Cetere , ĉiuj problemoj de la Projekto Euler ankaŭ povas esti solvitaj interrete en la rekomendinda retejo HackerRank .