Project Euler is a series of exciting programming problems that often have a mathematical background. the problems are often set up in such a way that you have to develop sophisticated algorithms to reach the goal in a reasonable runtime. today we solve problem 15: Lattice paths, where you get to the solution with simple combinatorial means.
The question is as follows:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
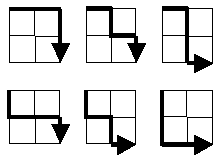
The problem can also be formulated differently: What is sought is the power of the subset of all paths
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
This is a simple combinatorial problem, where we use the urn model (without putting it back and without considering the order). We are now interested in exactly those paths for which \(R\) and \(D\) occur exactly the same number of times, so for all possible combinations:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
For \(n=20\) we get:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
We can extend the problem to non-square grids. The following solution implements a calculation in PHP with the help of bcmath with a runtime of \( O(n) \) with the input format "Number of test cases, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
By the way, all problems of the Euler Project can be solved online on the recommended page HackerRank.