Project Euler là một loạt các bài toán lập trình thú vị, thường có nền tảng toán học. Các vấn đề thường được đặt ra theo cách mà các thuật toán phức tạp phải được phát triển để đạt được mục tiêu trong thời gian chạy hợp lý. Hôm nay chúng ta giải quyết vấn đề 15: Đường dẫn mạng , nơi bạn có thể tìm thấy lời giải bằng các phương tiện tổ hợp đơn giản.
Câu hỏi như sau:
„Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?“
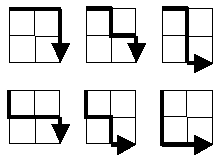
Vấn đề cũng có thể được xây dựng theo cách khác: Điều cần thiết là sức mạnh của tập con của tất cả các đường
$$W = {w_1, …, w_{2^n}}, \, w_k = p_1 \cdots p_{2\cdot n}, \, p_k \in \{ R, D \}.$$
Đây là một bài toán tổ hợp đơn giản, trong đó chúng ta sử dụng mô hình urn (không thay thế và không xét thứ tự). Bây giờ chúng tôi quan tâm đến chính xác những đường dẫn mà nó cho rằng \(R\) và \(D\) cùng một tần số. Điều này dẫn đến tất cả các kết hợp có thể có:
$$\binom{2\cdot n}{n} = \frac{(2\cdot n)!}{n!\cdot n!}$$
Đối với \(n=20\) chúng tôi nhận được:
$$ \frac{(40)!}{20!\cdot 20!} = 137846528820.$$
Chúng ta có thể mở rộng vấn đề sang các lưới không vuông. Giải pháp tiếp theo được thực hiện trong PHP bằng cách sử dụng bcmath với số hạng là \( O(n) \) một phép tính sử dụng lời nhắc "số lượng trường hợp thử nghiệm, \(n_1\) \(m_1\) , ...":
47bb78215ee0531a787bb5034652eaf4
Nhân tiện , tất cả các vấn đề của Dự án Euler cũng có thể được giải quyết trực tuyến trên trang HackerRank được đề xuất.